Кластеризация текстовых документов по семантическим признакам

Существует огромное количество алгоритмов кластеризации. Основная идея большинства из них – объединить одинаковые последовательности в один класс или кластер на основе сходства. Как правило, выбор алгоритма определяется поставленной задачей. Что касается текстовых данных, то здесь сравниваемыми составляющими служат последовательности слов и их атрибутов (например, вес слова в тексте, тип именованной сущности, тональность и пр.). Таким образом, тексты изначально преобразуются в вектора, с которыми производят разного типа манипуляции. При этом, как правило, возникает ряд проблем, связанных с: выбором первичных кластеров, зависимостью качества кластеризации от длины текста, определением общего количества кластеров и т.п. Но наиболее сложной проблемой является отсутствие связи между близкими по смыслу текстами, в которых используется разная лексика. В таких случаях объединение должно происходить не только на основе сходства, а еще и на основе семантической смежности или ассоциативности. 

Например, 

В Лондоне передумали объявлять России новую холодную войну
Борис Джонсон: Запад не находится в состоянии новой холодной войны с РФ
В британском МИД заявили, что Запад не хочет новой холодной войны с Россией

Все три примера являются одной новостью, тем не менее, лексика используется разная. В таких случаях уже не помогают алгоритмы кластеризации, основанные на лексическом сходстве.
Задачи такого типа решаются двумя путями: 1) составлением тезаурусов и 2) использованием разного рода «хитрых» алгоритмов, устанавливающих ассоциативно-семантические связи между словами, как-то: латентно-семантический анализ (LSA), вероятностный латентно-семантический анализ (pLSA), латентное размещение Дирихле (LDA) и т.п.

Первый путь – получение тезаурусов – достаточно трудоемок и полностью определяется поставленной задачей. Это значит, что создать универсальный тезаурус пока не представляется возможным. 

Второй путь – алгоритмический – также имеет свои недостатки. Прежде всего, это «туманность» самих методов и неочевидность их применения для текстовых данных. Скажем, LDA требует условия нормальности распределения, что при решении лингвистических задач не всегда удовлетворяется. Как правило, все эти алгоритмы имеют большое количество параметров, определение которых является эмпирическим и может существенно повлиять на качество решения (например, сокращение сингулярных значений диагональной матрицы в LSA очень нелинейно влияет на результат).

Мы попробовали обойти ряд вышеуказанных проблем, воспользовавшись результатами работы алгоритма Word2Vec. 

Word2Vec

Описание алгоритма можно найти в Википедии или другом информационном ресурсе. Алгоритм создавался, прежде всего, для поисковых задач, поэтому напрямую его использовать для других лингвистических целей нужно с аккуратностью.

Алгоритм имеет два способа обучения и несколько вариантов демонстрации результатов. Нас, в частности, будет интересовать представление результата classes – получение ассоциативно-семантических классов (с использованием k-mean, кстати).

Как показывают эксперименты, даже на небольших коллекциях в несколько миллионов словоупотреблений получаются более-менее «осмысленные» классы слов. Но как использовать такой результат, если у слов нет веса (например, предлоги и «ключевые» слова имеют одинаковое представление в такой модели)? Другой проблемой является то, что классы не идеальны и, например, служебные слова могут попасть в семантически значимый класс. Использовать стоп-лист? Тогда есть риск выплеснуть из корыта вместе с водой ребенка. Вообще применение стоп-списков имеет свои существенные недостатки (например, выкидывая местоимения, мы теряем общероссийское молодёжное общественное политическое движение «НАШИ»; выбрасывая однобуквенные слова, мы не обнаружим информации о «Ъ» — сокращение газеты «Коммерсантъ» и т.д.). 

Наконец, какое количество классов будет оптимальным для кластеризации текста? Зависит ли это от объема обучающей или тестовой выборки, тематики текста, его объема? На эти ключевые вопросы мы ответим во второй части публикации, а пока кратко опишем алгоритм.

Описание алгоритма

Идея алгоритма в сравнении не самих слов или составленных из них последовательностей (так называемых н-грамм), а семантических классов, в которые они попадают. 

Для обучения требуется большой объем текстового материала (сотни тысяч, а лучше десятки миллионов словоупотреблений; чем больше выборка, тем меньше тематическая привязка модели к тексту, тем реже нужно подстраивать под текст модель). В результате обучения получается список, где почти к каждому слову текста приписан какой-либо класс (количество классов указывается на этапе обучения). Затем этот список на основе частотных распределений слов в тексте и в соответствующем им классе приводится к формату: слово — класс — вес, сглаженный по определенному алгоритму. Здесь важными параметрами являются общее количество классов и коэффициенты сглаживания (более подробно во второй части публикации). 

Вот пример небольшого семантического класса.

кроху	дочку
мамочку	тещу
воспитательницу	дочу
детку	родню
учительницу	младшую
сестренку	жену
малышку	папину
сестру	бывшую
тетю	бабушку
бабулю	старшую
подружку	подругу
мамку	любовницу
супругу	гражданку
тётю	семью
внучку	девочку
девичью	мамину
ее

В этот более-менее однородный ассоциативно-семантический класс попадает местоимение «ее», которое, в принципе, уместно, но малоинформативно. Оно может помешать при кластеризации материала, поскольку частотно и «перетянет одеяло» на себя. Такие «выбросы» можно убрать последующим сглаживанием модели.

По полученной модели все слова из тестовой выборки преобразуются в цифры, соответствующие семантическим классам, и дальнейшие манипуляции происходят только с цифрами. Для кластеризации используется простой алгоритм сравнения накопленных документов между собой. Сравниваются целочисленные типы (int), поэтому скорость получается достаточно высокой. При этом на сравнение наложен ряд фильтров, типа ограничений по количеству семантических классов в одном документе, минимального количества документов в кластере, меры близости – количество совпавших классов. Логика алгоритма организована так, что один и тот же документ может попадать в разные кластеры (поскольку первичные кластеры не определены). Вследствие такой «нечеткости» первичный результат представляет собой достаточно объемный набор близких по тематике кластеров. Поэтому требуется пост кластеризация, которая просто объединяет близкие кластеры, сравнивая их по количеству одинаковых документов (по их id). 

Таким образом, используя вышеописанную логику, удается достичь не только высокой скорости кластеризации, но и не заморачиваться ни определением первичных кластеров, ни общим их количеством.

Результаты и выводы

В кластеризации сложно говорить о качестве результата, поскольку это сильно зависит от кластеризуемого материала. В этом смысле делать «золотой» стандарт особого резона нет. Но есть смысл проверить модели на разных корпусах для классификации (о чем речь пойдет, опять же, во второй части статьи). 

Как показали тесты по классификации документов векторным методом на униграммах (сравнение по косинусу), модели кластеризации почти не уступают в точности моделям на «словах». Это значит, классификация «без учителя» (модели в этом смысле универсальны) может показывать результаты лишь немного хуже, чем полноценное обучение с учителем. Ухудшение составляет 1-10% и зависит от тестируемого материла. Но это ведь и не является целью! Просто это значит, что модели кластеризации, полученные с помощью алгоритма Word2Vec вполне валидны для их применения на любом типе материала с любым количеством классов (в данном случае кластеров). 

Качество результата определяется фильтрующими порогами: например, если нам нужно просто выявить нечеткие дубли, то нужно задать более жесткие параметры; и наоборот, если нужно просто посмотреть основные тематики выходящего материала, то можно выставить более мягкие параметры. 

В целом, алгоритм универсален: он может работать на любом количестве материала. Хотя при больших объемах лучше работать окнами по 10-100 тысяч документов; полученные таким образом первичные кластеры затем объединяются в пост кластеризации. Алгоритм так же слабо чувствителен к длине документа: желательно, чтобы «длинные» документы были семантически однородны (принадлежали одной теме). 

Тем не менее, в данном алгоритме существует ряд проблем. Прежде всего, это зависимость результата от количества классов в модели: иногда это может стать чувствительным, особенно для «слабых» кластеров, т.е. кластеров с небольшим объемом документов. Вторая проблема следует из-за неидеального определения семантических классов, вследствие чего иногда близкие по смыслу документы попадают в разные кластеры (отличающиеся, скажем, парой классов). Такие проблемы устраняются дополнительным пост объединением, основанным на факторизации документов: выделении именованных объектов и связей между ними. Но такая задача решается уже проще, ибо количество кластеров небольшое относительно первичного объема документов и большая часть из них уже объединена. 

Таким образом, представленный алгоритм имеет ряд преимуществ:

• кластеризация происходит не по словам, а семантическим классам;
• независимость результата от длины документов;
• независимость результатов от объема материала;
• автоматическое определение количества кластеров;
• отсутствие необходимости определения первичных кластеров;
• высокая скорость работы, что позволяет использовать данный алгоритм на большом потоке текстовых сообщений.

Несмотря на то, что алгоритм не чувствителен к объему входящего материала, его рекомендуется использовать для кластеризации больших потоков неструктурированной информации, когда важны не только качество кластеризации, но и скорость получения результата. Для небольших объемов тематически обособленного материала (например, фармацевтики, игровых чатов и т.п.) лучше использовать тезаурусы, поскольку модель Word2Vec может не содержать профессиональную терминологию или узкоспециализированный жаргон.

Модели Word2Vec

Модели получаются из classes — представления результата текста word2vec виде ассоциативно-семантических классов путем сглаживания распределений.

Идея сглаживания в следующем. 

1. Получаем частотный словарь обучающего материала, где каждому слову приписана его частота встречаемости по документам (т.е. в скольких документах это лексема встретилась).
2. На основе этого частотного распределения для каждого слова класса считается его среднеквадратичное отклонение (или дисперсия, в данном случае не имеет принципиальной разницы).
3. Для каждого класса считаем среднее по всем отклонениям его составляющих.
4. Из каждого класса убираем «выбросы» — слова с большим среднеквадратичным отклонением:

 

Где SDw – среднеквадратичное отклонение каждого слова, avr(SDcl) – среднее среднеквадратичное по классу, k – коэффициент сглаживания.

Очевидно, что результат будет зависеть от коэффициента k. Его выбор – задача эмпирическая, он зависит от языка, объема обучающей выборки, ее однородности и пр. Но все-таки какие-то общие вещи попробуем выявить.

Построение и тестирование моделей

Для моделей использовался материал, собранный из дневного потока интернет, собранный по спискам наиболее частотных ключевых слов. Английский текст содержал около 170 млн. словоформ, русский – чуть менее миллиарда. Диапазон количества классов был от 250 до 5000 классов с шагом 250. Остальные параметры были использованы по умолчанию. 

Тестирование проводилось на русскоязычном и англоязычном материале. 

Методика тестирования в двух словах следующая: брались эталонные тестовые корпуса для классификации и прогонялись через модели кластеризации с различными параметрами: меняя количество классов и сглаживающий коэффициент можно продемонстрировать динамику изменения результата, а, следовательно, качества модели.

Английские пять корпусов взяты из открытого источника: 

• 20NG-TEST-ALL-TERMS – 20 тем (10555K)
• MINI20-TEST – 20 тем (816K)
• R52-TEST-ALL-TERMS – 52 темы (1487K)
• R8-TEST-ALL-TERMS – 8 тем (1167K)
• WEBKB-TEST-STEMMED – 4 темы (1271K)

Русские корпуса пришлось использовать из закрытых разработок, поскольку открытых источников обнаружить не удалось:

• Ru1 — Корпус коротких сообщений – 13 тем (76K)
• Ru2 — Новостной корпус – 10 тем (577K)

При тестировании использовался простейший метод сравнения, без использования каких-либо сложных метрик. Выбор в пользу такой простейшей классификации (Dumb classifier) был сделан в виду того, что целью исследования было не улучшение результата классификации, а сравнительный анализ результатов при разных входящих параметрах. То есть был интересен не сам результат, а его динамика.

При этом на некоторых моделях кластеризации были проведены тесты с использованием логарифмической меры TFiDF, чтобы проверить, насколько в принципе эти результаты на этих моделях могут отличаться от результатов на моделях, обученных на лексических униграммах. Такие тесты показали, что результаты на моделях с ассоциативно-семантическими классами почти не уступают моделям на униграммах: наблюдалось небольшое ухудшение качества от 1 до 10%, в зависимости от тестового корпуса. Что говорит о конкурентоспособности полученных моделей кластеризации, учитывая, что они изначально не «заточены» под тематики.

Зависимость качества модели от количества классов

Со всеми корпусами были проведены тесты с разным количеством семантических классов: от 250 до 5000 с шагом 250 классов.

На рисунках 1 и 2 продемонстрированы зависимости точности классификации от количества классов моделей для русского и английского языков.

Рис.1. Зависимость точности классификации от количества семантических классов word2vec для русскоязычных корпусов. По оси абсцисс – количество классов, по оси ординат – значения точности. 

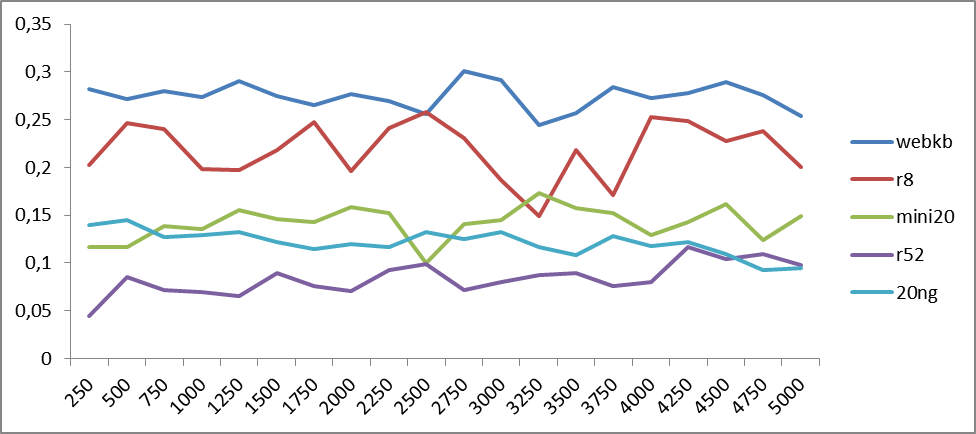
Рис.2. Зависимость точности классификации от количества семантических классов word2vec для англоязычных корпусов. По оси абсцисс отложены количество классов, а по оси ординат – точность классификации.

Из графиков видно, что колебания точности имеют периодический характер, период которых может разниться в зависимости от тестируемого материала. Что бы определить тенденции, построим графики средних значений. 

Рис.3. Среднее значение зависимость точности классификации от количества семантических классов word2vec для русскоязычных корпусов. По оси абсцисс – количество классов, по оси ординат – значения точности. Добавлена полиномиальная (6-ой степени) линия тренда.

Рис.4. Среднее значение зависимость точности классификации от количества семантических классов word2vec для англоязычных корпусов. По оси абсцисс – количество классов, по оси ординат – значения точности. Добавлена полиномиальная (6-ой степени) линия тренда.

Из рисунков 3 и 4 уже видно, что качество результата в среднем растет с увеличением количества классов в диапазоне от 4 до 5 тысяч. Что, вообще говоря, не удивительно: более тонкое разбиение пространства приводит к его конкретизации. Но дальнейшее разбиение может привести к тому, что семантические классы начинают расслаиваться на однородные куски. А это уже приводит к падению точности, ибо классы перестают «зацепляться»: одному и тому же смыслу будут соответствовать разные семантические классы. Это и наблюдается в приближении к 5 тысячам классов как для русского, так и для английского языков.

Любопытны пики, имеющиеся на обоих рисунках в районе 500 классов: несмотря на то, что семантических классов мало (следовательно, классы перемешаны), тем не менее, наблюдается макро-семантическое объединение: классы в целом тяготеют к той или иной теме.

Из полученных результатов можно сделать вывод, что все-таки более оптимальное разбиение может находиться где-то между 4-ю и 5-ми тысячами классов.

Зависимость качества модели от сглаживающего коэффициента.

На рисунке 5 показаны изменения точности классификации для корпуса R8 при разных коэффициентах сглаживания (для 1500 классов). Периодичность изменений для любого количества классов в пределах одного корпуса одинакова. Подобные графики наблюдаются для всех корпусов.

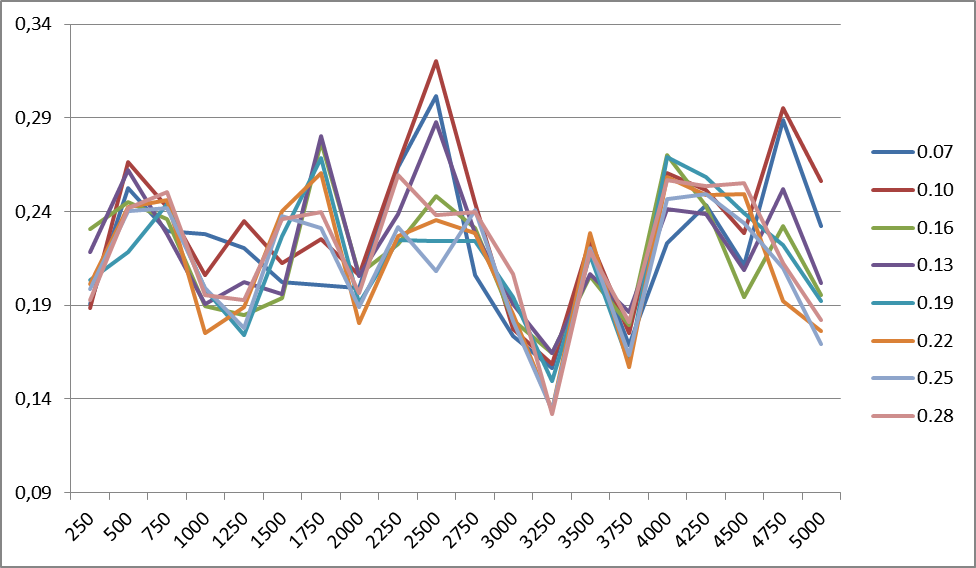
Рис.5. Изменения точности классификации для корпуса R8 при разных значениях коэффициента сглаживания. Справа приведены значения коэффициента сглаживания.

Что бы выявить основные тенденции, построим графики средних значений точности сглаживающего коэффициента по всем корпусам для английского и русского языков.

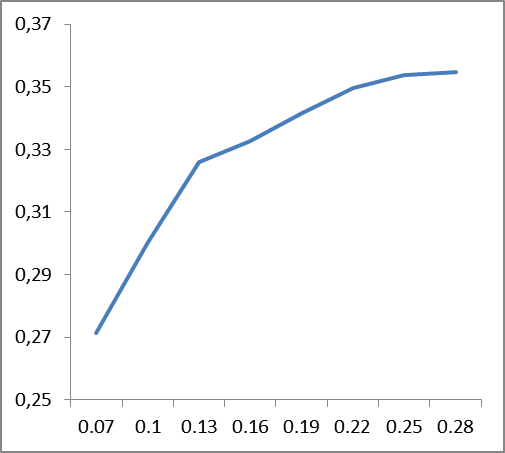Рис 6. Зависимость изменения точности классификации (по вертикали) от значений сглаживающих коэффициентов (по горизонтали), усредненные данные по корпусам: слева – для английского языка, справа – для русского. 

Из графиков, представленных на рис. 6 следует, что сглаживающий коэффициент языкозависим: если для английского языка стабильность наступает где-то около значения 0.22, то для русского это около 0.12. По всей видимости, это должно быть как-то связано со сложностью языка, его перплексией. 

Сложно сказать, чем объясняется пик точности в начале (0.07) для английского языка. Его наличие вызвано поведением корпуса R8, и, возможно, обусловлено лексическим наполнением самого корпуса.

На самом деле, если сравнить сами данные моделей при разных коэффициентах сглаживания, то видно, что при вышеуказанных порогах часть высокочастотных слов (предлоги, союзы, артикли) фильтруется. Поэтому нет смысла вводить стоп-списки: данная лексика либо фильтруются, либо образуют отдельный ассоциативно-семантический класс с достаточно низким весом.

Зависимость вариабельности сглаживающего коэффициента от количества классов очень слабо влияет на изменение точности. При этом не удалось выявить какой-либо тенденции такого влияния для разного материала.

Выводы

Разумеется, это не единственный, и возможно, не самый лучший метод получения моделей, ибо является эмпирическим и зависит от множества факторов. К тому же сглаживание можно провести куда более хитрыми способами. Тем не менее, данный метод позволяет быстро и качественно построить модели и получать неплохие результаты кластеризации на больших объемах информации. 

Приведем пример использования кластеризации на русскоязычном материале.

Пример

Кластеризация потока сообщений соц.медиа с поисковым запросом «Сбербанк». Количество сообщений – 10 тысяч. Это примерно 10 МБ текста или 5-6 часов потока сообщений по теме Сбербанк.

В итоге получилось 285 кластеров, откуда сразу видно основные события, касающиеся Сбербанка.
Вот, к примеру, первые десять кластеров (заголовки первых сообщений):

1. клиенты Сбербанка пожаловались на сбои в работе онлайн-сервиса — подобного рода 327 сообщений
2. жиды хотят приватизировать Сбербанк в ближайшие 3 года – 77 сообщений
3. ответы Сбербанка, типа: <имя> здравствуйте, к сожалению, в настоящий момент действительно есть перебои в работе… — 74 сообщения
4. Сбербанк в 2017 году проведет тест квантовой передачи информации hi-tech – 73 сообщения
5. в год своего 175-летнего юбилея Сбербанк дарит бесплатный вход в художественные музеи – 71 сообщений
6. узнай о преимуществах молодежной дебетовой карты visa сбербанк и как купить толстовку за n рубль – 57 cообщений
7. Минэкономразвития предложил включить Сбербанк в план приватизации – 58 сообщений
8. Сбербанк сообщил о сбоях в работе своих систем – 60 сообщений
9. Владимир Путин принял участие в конференции вперед в будущее роль и место России – 61 сообщение (Сбербанк так же принял участие);
10. Греф опроверг информацию о приватизации сбербанка — 64 сообщения

Скорее всего, 1-ый и 8-ой кластеры можно объединить в макро кластеры на основе дополнительной информации, например, использование гео-меток, источников сообщений, предикативных отношений между объектами и пр. Но это уже другая задача, о которой расскажем в следующий раз.

Ознакомиться с примерами и демо-реализацией алгоритма можно тут.