Сегодня разговор пойдёт о ещё одном вероятностном-рандомизированном алгоритме, который позволяет с минимальными затратами памяти определить примерное число уникальных элементов в больших объёмах данных.
Для начала, поставим себе задачу: предположим, что у нас имеется большой объём текстовых данных — скажем, плоды литературного творчества небезызвестного Шекспира, и нам необходимо подсчитать количество различных слов встречающихся в этом объёме. Типичное решение — счётчик с урезанной хеш-таблицей, где ключами будут слова без ассоциированных с ними значений.
Способ всем хорош, но требует относительно большой объём памяти для своей работы, ну а мы с вами, как известно, неугомонные гении эффективности. Зачем много, если можно мало — примерный размер словарного запаса упомянутого выше Шекспира, можно вычислить используя всего 128 байт памяти.
Идея
Как обычно нам понадобится какая-нибудь хеш-функция, соответственно на вход алгоритму будут поступать не сами данные, а их хеши. Задача хеш-функции, как это обычно и бывает в рандомизированных алгоритмах, состоит в превращении упорядоченных данных в «случайные», то-бишь в более-менее равномерном размазывании области определения по области значений. Для тестовой реализации я выбрал FNV-1a, как неплохую и простую хеш-функцию:
function fnv1a(text)
{
var hash = 2166136261;
for (var i = 0; i < text.length; ++i)
{
hash ^= text.charCodeAt(i);
hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24);
}
return hash >>> 0;
}Ну что ж, включим мозг и посмотрим на хеши, которые она выдаёт в двоичном представлении:
fnv1a('aardvark') = 10011000000000011101001000110011
fnv1a('abyssinian') = 00101111000100001010001000111100
fnv1a('accelerator') = 10111011100010100010110001010100
fnv1a('accordion') = 01110101110001001110100000011001
fnv1a('account') = 00101001010011111100011101011100
fnv1a('accountant') = 00101010011011111100111100101101
fnv1a('acknowledgment') = 00001010000100111000001111101000
fnv1a('acoustic') = 11110011101011111110010101100010
fnv1a('acrylic') = 11010010011100110111010111011000
fnv1a('act') = 00101101010010100100010110001011
Обратим внимание на индекс первого ненулевого младшего бита для каждого хеша, прибавим к этому индексу единицу и назовём это рангом (rank(1) = 1, rank(10) = 2, …):
function rank(hash)
{
var r = 1;
while ((hash & 1) == 0 && r <= 32) { ++r; hash >>>= 1; }
return r;
}Вероятность того, что мы встретим хеш с рангом 1 равна 0.5, с рангом 2 — 0.25, с рангом r — 2—r. Иначе говоря, среди 2r хешей обязан встретиться один хеш ранга r. Совсем иначе говоря, если запоминать наибольший обнаруженный ранг R, то 2R сгодится в качестве грубой оценки количества уникальныхэлементов среди уже просмотренных.
Ну, теория вероятностей штука такая, что мы можем обнаружить большой ранг R в маленькой выборке, а можем и маленький в преогромнейшей выборке, и вообще 231 и 232 — это две большие разницы, скажите вы и будете правы, именно поэтому такая единичная оценка очень груба. Что же делать?
Можно вместо одной хеш-функции использовать пачку оных, а потом каким-то образом «усреднить» оценки полученные по каждой из них. Такой подход плох тем, что функций нам потребуется много и их все придётся считать. Поэтому сделаем следующую хитрость – будем отгрызать k старших битов у каждого из хешей и, используя значение этих битов в качестве индекса, будем вычислять не одну оценку, а массив из 2k оценок, а затем на их основе получим интегральную.
HyperLogLog
На самом деле, существует несколько вариаций алгоритма LogLog, мы рассмотрим относительно свежий вариант — HyperLogLog. Эта версия позволяет достичь величины стандартной ошибки:
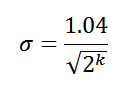
Следовательно, при использовании 8 старших битов в качестве индекса, мы получим стандартную ошибку в 6.5% (σ = 0.065) от истинного числа уникальных элементов. И самое главное, если вооружиться мэд скилзами по теории вероятностей, можно прийти к следующей финальной оценке:
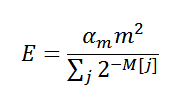
, где αm — корректирующий коэффициент, m — общее количество оценок (2k), M — массив самих оценок. Теперь мы знаем почти всё, пришло время для реализации:
var pow_2_32 = 0xFFFFFFFF + 1;
function HyperLogLog(std_error)
{
function log2(x)
{
return Math.log(x) / Math.LN2;
}
function rank(hash, max)
{
var r = 1;
while ((hash & 1) == 0 && r <= max) { ++r; hash >>>= 1; }
return r;
}
var m = 1.04 / std_error;
var k = Math.ceil(log2(m * m)), k_comp = 32 - k;
m = Math.pow(2, k);
var alpha_m = m == 16 ? 0.673
: m == 32 ? 0.697
: m == 64 ? 0.709
: 0.7213 / (1 + 1.079 / m);
var M = []; for (var i = 0; i < m; ++i) M[i] = 0;
function count(hash)
{
if (hash !== undefined)
{
var j = hash >>> k_comp;
M[j] = Math.max(M[j], rank(hash, k_comp));
}
else
{
var c = 0.0; for (var i = 0; i < m; ++i) c += 1 / Math.pow(2, M[i]);
var E = alpha_m * m * m / c;
// -- make corrections
if (E <= 5/2 * m)
{
var V = 0; for (var i = 0; i < m; ++i) if (M[i] == 0) ++V;
if (V > 0) E = m * Math.log(m / V);
}
else if (E > 1/30 * pow_2_32) E = -pow_2_32 * Math.log(1 - E / pow_2_32);
// --
return E;
}
}
return {count: count};
}
function fnv1a(text)
{
var hash = 2166136261;
for (var i = 0; i < text.length; ++i)
{
hash ^= text.charCodeAt(i);
hash += (hash << 1) + (hash << 4) + (hash << 7) + (hash << 8) + (hash << 24);
}
return hash >>> 0;
}
var words = ['aardvark', 'abyssinian', ..., 'zoology']; // 2 336 words
var seed = Math.floor(Math.random() * pow_2_32); // make more fun
var log_log = HyperLogLog(0.065);
for (var i = 0; i < words.length; ++i) log_log.count(fnv1a(words[i]) ^ seed);
var count = log_log.count();
alert(count + ', error ' + (count - words.length) / (words.length / 100.0) + '%');Прикинем, сколько байт памяти мы используем, k равно 8, следовательно, массив M состоит из 256 элементов, каждый из них, условно, занимает 4 байта, что в сумме составляет 1 Кбайт. Неплохо, но хотелось бы меньше. Если задуматься, размер единичной оценки из массива M можно уменьшить — необходимо всего ceil(log2(32 + 1 — k)) битов, что, при k = 8, есть 5 бит. В сумме имеем 160 байт, что уже гораздо лучше, но я обещал ещё меньше.
Чтобы было меньше, необходимо заранее знать максимальное возможное количество уникальных элементов в наших данных — N. И действительно, если мы его знаем, нет никакой необходимости использовать все возможные биты из хеша для определения ранга, достаточно ceil(log2(N/m)) битов. Не забываем, что от этого числа нам ещё раз нужно взять логарифм, чтобы получить размер одного элемента массива M.
Предположим, что, в случае с нашим небольшим набором слов, максимальное их количество составляет 3 000, тогда нам необходимо всего 64 байта. В случае с Шекспиром, положим N равным 100 000, и будем иметь обещанные 128 байт при ошибке в 6.5%, 192 байта при 4.6%, 768 при 3.3%. Кстати, реальный размер словарного запаса Шекспира составляет около 30 000 слов.
Прочие мысли
Конечно, использовать мелкие «байты», например, по 3 бита не очень эффективно с точки зрения производительности. На практике лучше не сходить с ума выстраивая довольно длинные цепочки битовых операций, а применить обычные родные для архитектуры байты. Если вы всё-таки решитесь «мельчить», не забудьте поправить корректирующий оценку код.
Небольшая ложка дёгтя, ошибка σ — это не максимальная ошибка, а, так называемая, стандартная ошибка. Для нас это означает, что 65% результатов будут иметь ошибку не более σ, 95% — не более 2σи 99% — не более 3σ. Вполне приемлемо, но всегда есть вероятность получить ответ с ошибкой больше ожидаемой.
Судя по моим экспериментам, не следует слишком увлекаться её уменьшением, особенно если данных предполагается мало. В этом случае, начинает работать процедура коррекции, которая не всегда справляется со своими обязанностями. Похоже, алгоритм требует тестирования и настройки под конкретную задачу, если, конечно, это не какая-то глупая ошибка в моей реализации. Это не совсем так.
При использовании хеш-функции шириной 32 бита, алгоритм позволяет подсчитать до 109 уникальных элементов при минимальной достижимой стандартной ошибке около 0.5%. Памяти, при такой ошибке, понадобиться порядка 32-64 Кбайт. В целом, LogLog идеально подходит для on-line работы с живыми потоками данных.