Nested Set

Хранение иерархических структур при помощи модели вложенных множеств

Создание модели для хранения иерархических данных — совсем непростая задача. Что же мы подразумеваем под иерархическими данными? Представьте, что вам необходимо организовать список продуктов по категориям. Например, у вас будет несколько основных категорий: продукты, оборудование, электроника. А далее вам потребуется разбить их на подкатегории, а те в свою очередь, на более узкие категории. На бумаге всё выглядит довольно просто, а вот в таблице СУБД (система управления базами данных) дело обстоит совсем по другому. В этой статье я попробую рассказать об основной идее этой модели и когда её следует применять. Начну с объяснения более простой иерархической модели, а далее перейдём к модели вложенных множеств.

Модель родитель-ребенок

Традиционно, иерархическая структура это модель, где четко отслеживается связь родителей и потомков. В случает с древовидной структурой каждый узел будет иметь уникальный ID и ID своего родителя. Сами ID не имеют никакого отношения к данным, они все лишь служат уникальными определителями узла. Корень дерева должен иметь специальное значение ID родительского узла, так как у корня родителей нет.

Рассмотрите следующую схему:

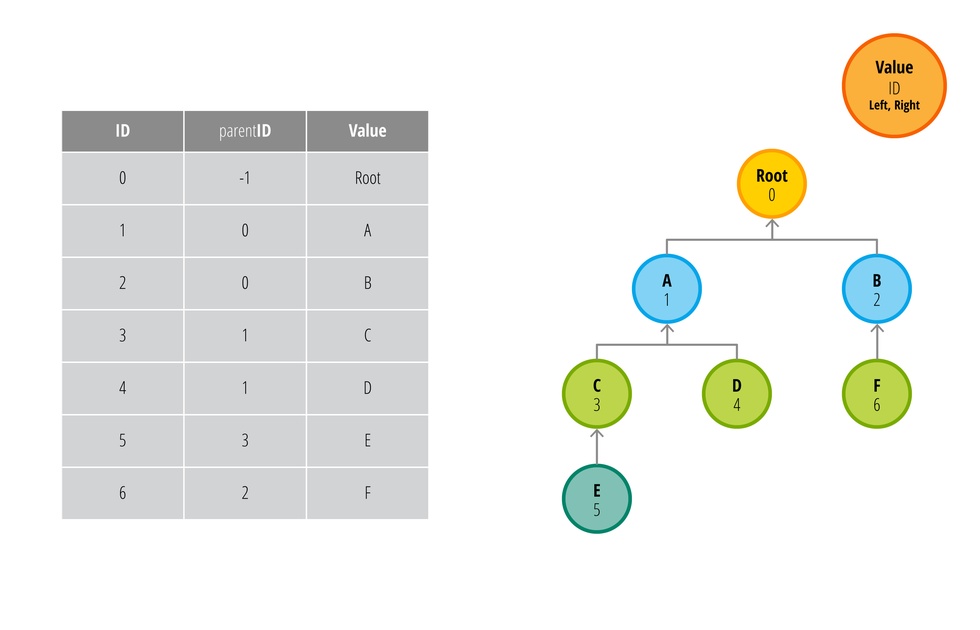
Каждая стрелка указывает на родителя узла в соответствии со значениями ID, parentID и Value из таблицы. Такая модель наиболее часто используется для представления иерархических структур. В каждом узле присутствует информация о его родителе и потомках.

Проблема

К сожалению, возникают проблемы при использовании такой модели, если мы хотим получить все дочерние элементы одного узла. Допустим, нам необходимо получить ID всех дочерних узлов элемента с ID равным 1. Взглянув на наше схему, мы можем смело сказать, что это узлы 3, 4 и 5. Но при использовании таблицы базы данных сделать это не так просто.

Получаем дочерние узлы

Сначала получим все узлы, родителем которых является узел с ID равным 1. В нашем случае это узлы 3 и 4 (Цифра на жёлтых стрелках показывает номер запроса к БД). Теперь надо получить дочерние элементы узлов 3 и 4. Не трудно заметить, что такой способ приведет к сотням, а то и тысячам запросов к базе данных при использовании большого количества данных. Обратите внимание на то, что количество необходимых запросов пропорционально высоте дерева. Нам всегда придется выполнить на один запрос больше, чем высота дерева данных.

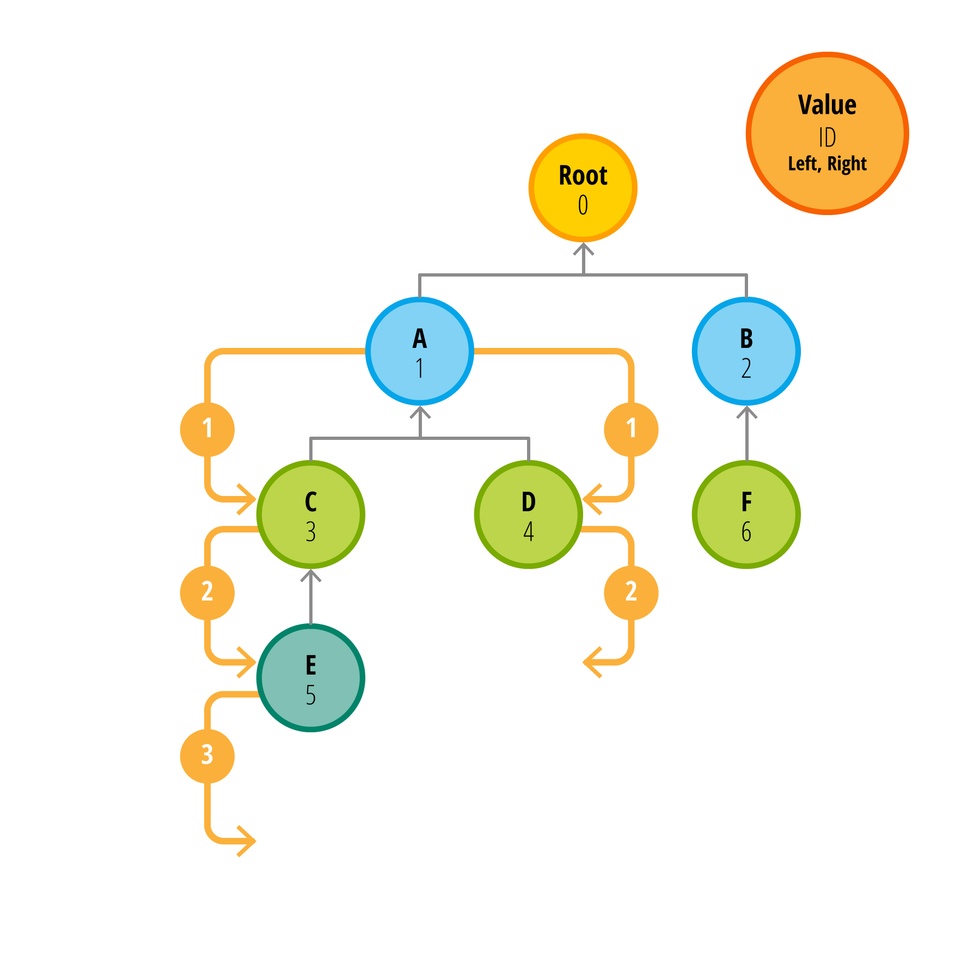
Вложенные множества — решение проблемы (Nested Set)

Вот тут то нам и пригодится идея вложенных множеств. Эта модель не такая простая как предыдущая, так что попробуем совместными усилиями в ней разобраться . Вместо ID родителя мы будем хранить значения левого и правого значения узла. Посмотрите на таблицу и схему ниже:

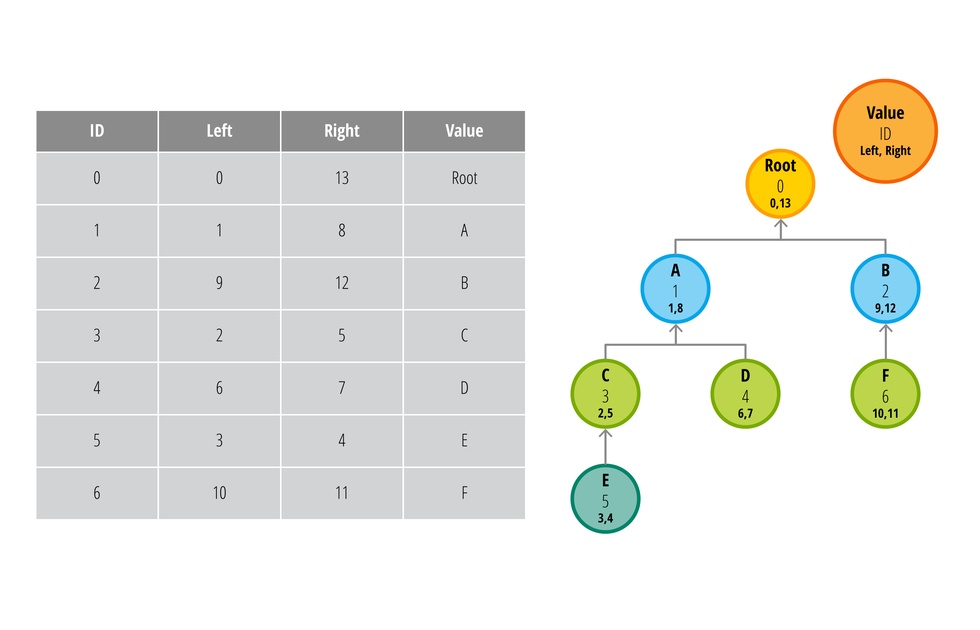
Вот это да? Что случилось?

Так, спокойно. Давайте вернемся на шаг назад и разберем как так получилось. Значение left и rightхранят ссылки на дочерние узлы. В свою очередь дочерние узлы тоже имеют такие переменные, отсюда и взялось определение вложенных множеств. Например, если бы мне надо было получить все дочерние элементы узла А (ID = 1), я бы выполнил следующий запрос:

SELECT * FROM `nodes` WHERE `Left` > 1 AND `Right` < 8;

В ответ я бы получил узлы C, D и E. Обратите внимание, что мы обошлись без рекурсии, нам хватило всего лишь одного запроса.

Все отлично, но как же определить значения left и right для построенного дерева?

На удивление, это совсем не трудно. Вот схема алгоритма этой процедуры:

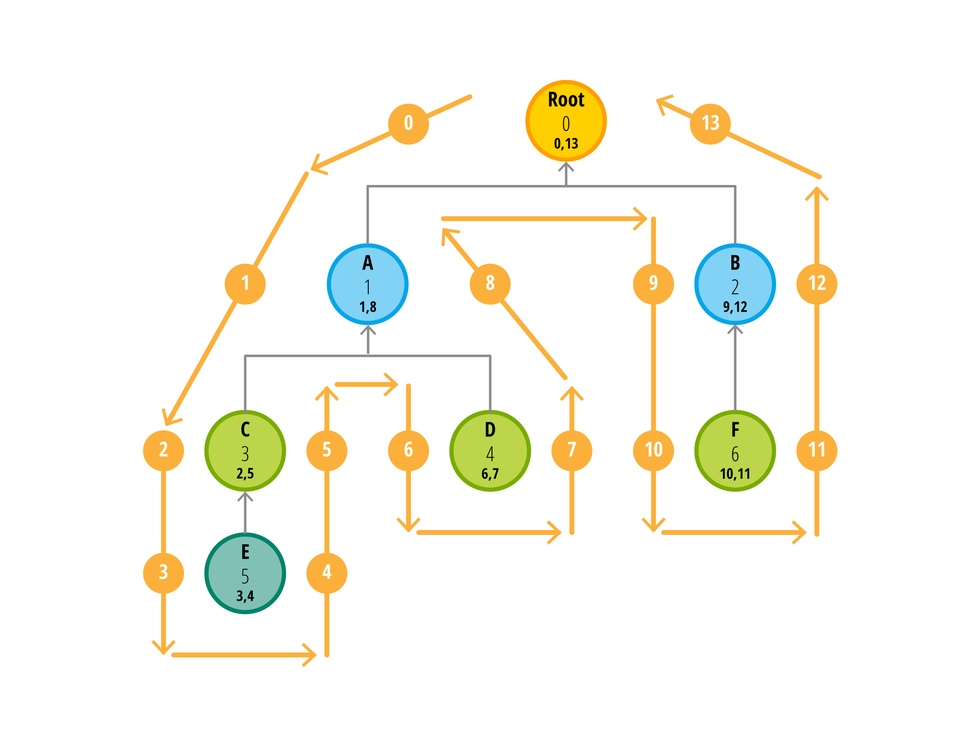
Определение значений right и left

Начните с верхней левой стрелки и счетчика равного 0. При прохождении узла увеличивайте счетчик на 1 и вписывайте его в узел. Если вы слева от узла, то значение счетчика представляет собой значение left, а если вы справа, то right.

Обратите внимание на то, что если у узла нет дочерних элементов, то значения left и right отличаются на единицу, а если же есть, то разница в значениях как минимум три, а по мере углубления вложенности увеличивается на два. Эта информация о многом нам говорит без использования дополнительных запросов к БД.

Альтернативное представление

Давайте попробуем более осмыслено взглянуть на эту структуру данных:

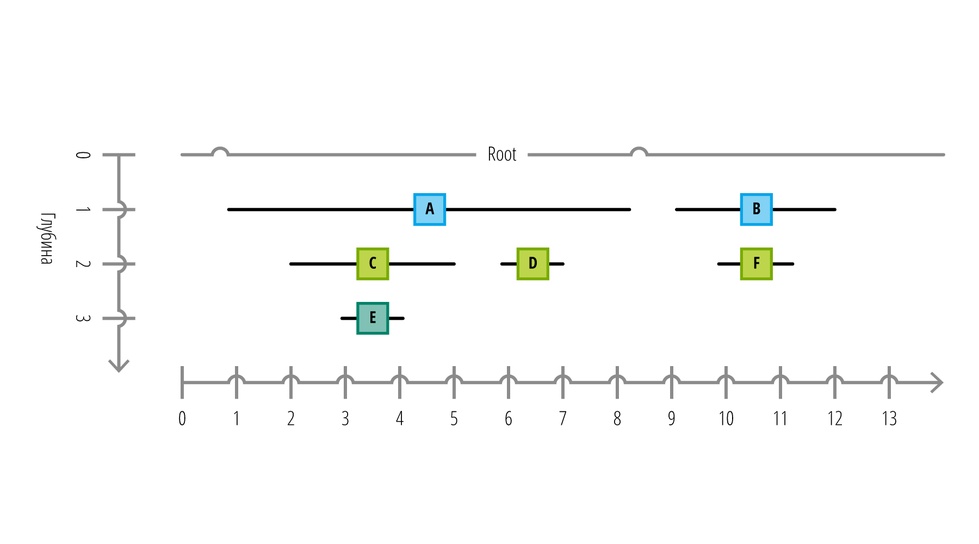
Из такой схемы мы можем легко определить структуры множеств и глубину их вложенности (расстояние до корня). Нижняя координатная прямая представляет собой одно измерение, в котором расположены все узлы. ID каждого следующего узла увеличивается на единицу, а также каждый узел имеет буфер для хранения данных. Если бы мы снова сделали запрос, чтобы получить все дочерние элементы узла A, то наш запрос принял бы следующий вид:

SELECT * FROM `nodes` WHERE `Left` > 1 AND `Right` < 8;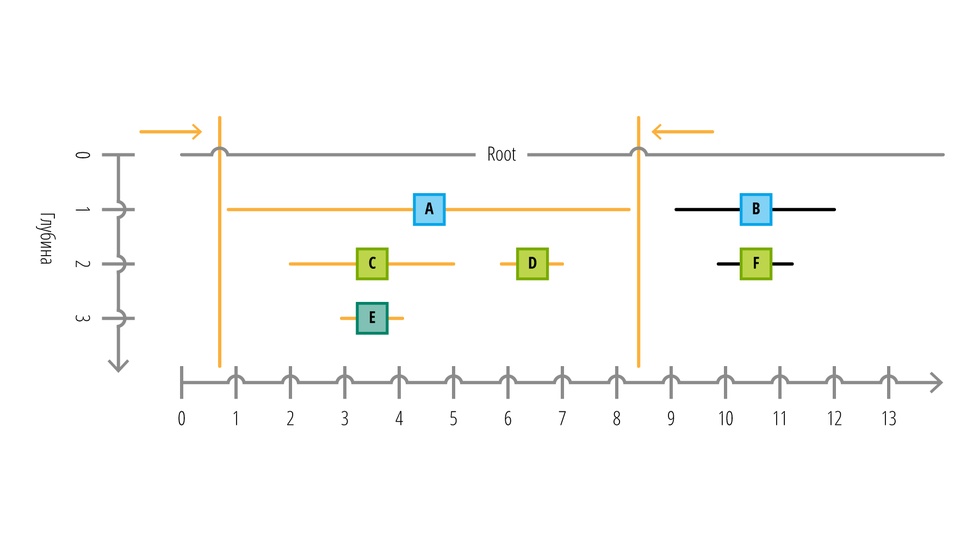

Добавление узлов

Давайте добавим новый узел со значение G сразу же после корня дерева (root узел). Посмотрите на таблицу и схему ниже:

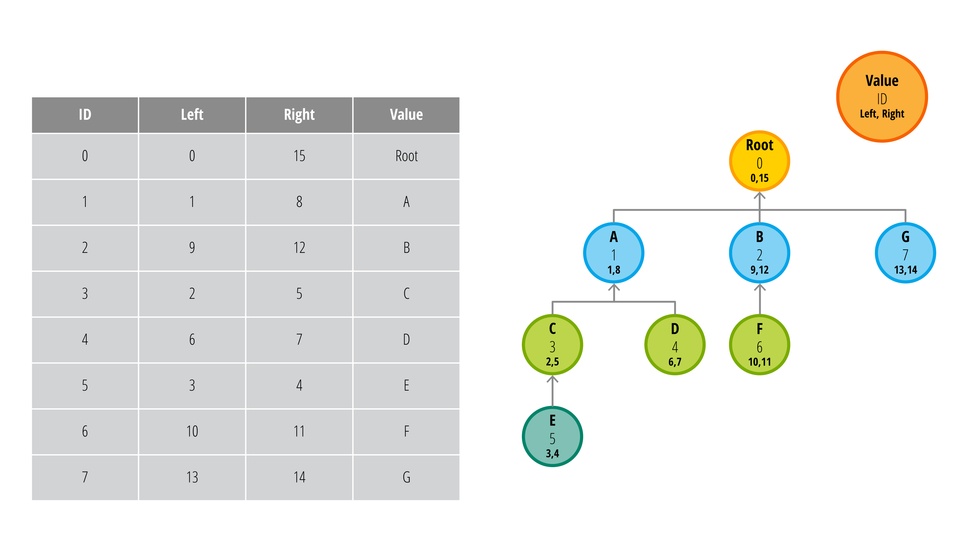
Чтобы добавить узел в качестве прямого потомка другого узла, сначала надо выделить пространство в дереве. Для этого получаем значение right исходного узла. В нашем случае это 13. Чтобы выделить требуемое пространство, прибавьте 2 ко всем значениям right и left, которые больше 13.

UPDATE `nodes` SET `Left` = `Left` + 2 WHERE `Left` > 13;
UPDATE `nodes` SET `Right` = `Right` + 2 WHERE `Right` > 13

Так как мы добавляем узел сразу же после корня, обновление значений left не требуется (мы добавляем узел G в качестве наследника корня с правой стороны, чтобы минимизировать количество запросов к БД. Попробуйте добавить узел с левой стороны и посмотрите сколько значений вам придется обновить). После того, как вы выделили требуемое пространство, добавьте ваш узел, указав левое значение равное правому значению root узла, а правое значение равное тому же значению плюс единица.

INSERT INTO `nodes` (`Left`, `Right`, `Value`) VALUES (13, 14, 'G');

Как удалять узлы?

Удаление узлов — очень простая операция. Разберем несколько возможных вариантов:

Удаление конечного узла (у которого нет потомков)

Удаляете конечный узел, а остальная часть дерева остаётся неизменной

1. Уменьшите все left значения на 2, которые больше left значения удалённого узла
2. Уменьшите все right значения на 2, которые больше right значения удалённого узла
3. Удалите сам узел

Удаление узла E

UPDATE `nodes` SET `Left` = `Left` - 2 WHERE `Left` > 3;
UPDATE `nodes` SET `Right` = `Right` - 2 WHERE `Right` > 4;
DELETE FROM `nodes` WHERE `id` = 5;

Удаление узла с потомками

1. Уменьшите значения left и right на единицу, если left значение больше левого значения удаляемого узла, а right значение — меньше правого.
2. Уменьшите все left значения на 2, если они больше значения left удаляемого узла.
3. Уменьшите все right значения на 2, если они больше значения right удаляемого узла.
4. Удалите узел.

Удаление узла A

UPDATE `nodes` SET `Left` = `Left`- 1 WHERE `Left` >= 1 AND `Right` <= 8;
UPDATE `nodes` SET `Right` = `Right`- 1 WHERE `Left` >= 1 AND `Right` <= 8;
UPDATE `nodes` SET `Left` = `Left` - 2 WHERE `Left` >= 8;
UPDATE `nodes` SET `Right` = `Right` - 2 WHERE `Right` >= 8;
DELETE FROM `nodes` WHERE `id` = 1;

Удаление корневого узла

Выглядит также как и удаления узла с потомками, за исключением того, что в итоге мы можем получить не одно, а несколько деревьев. Если у корня было несколько потомков, то в итоге они станут корневыми узлами. Обычно это не очень хорошо, но иногда такое поведение необходимо.

Пример удаления

Давайте посмотрим как выглядит удаление узла с потомками (узел А, индекс 1):

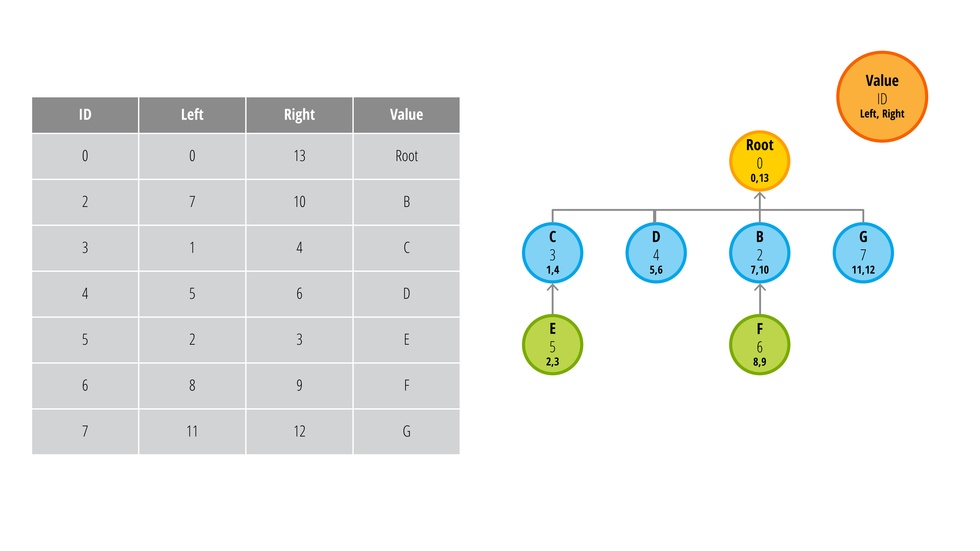
Заметьте, узлы C и D стали потомками корневого узла, а узел E остался потомком C. Если бы мы продолжили и удалили корневой узел, то получили бы в итоге 4 корневых узла и 2 потомка (обычно такой итог считается ошибкой, но опять таки все зависит от поставленной задачи).

Эффективность

Вложенные множества очень эффективны при получении списка потомков элемента. Но есть и свои минусы, например, при удалении или добавлении узла эта модель проигрывает, так как необходимо выполнять большое количество обновлений данных в БД. Даже если вы и обойдётесь всего тремя запросами SQL для вставки записи, то количество запросов для обновления узла может быть достаточно велико, что может сказаться на быстродействии БД.

Заключение

Принимайте модель вложенных множеств как дополнительный способ хранения иерархических данных. Эта модель очень эффективна при доступе к данным и довольна проста для добавления и удаления узлов, хотя и довольно ресурсоёмкая. При встрече со множествами попробуйте реализовать решение своей проблемы как через модель вложенных множеств, так и через стандартный метод родитель-потомок.