Структура данных (англ. data structure) — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных в вычислительной технике. Для добавления, поиска, изменения и удаления данных структура данных предоставляет некоторый набор функций, составляющих её интерфейс.
Термин «структура данных» может иметь несколько близких, но тем не менее различных значений:
- Абстрактный тип данных;
- Реализация какого-либо абстрактного типа данных;
- Экземпляр типа данных, например, конкретный список;
- В контексте функционального программирования — уникальная единица (англ. unique identity), сохраняющаяся при изменениях. О ней неформально говорят как об одной структуре данных, несмотря на возможное наличие различных версий.
Структуры данных формируются с помощью типов данных, ссылок и операций над ними в выбранном языке программирования.
Различные виды структур данных подходят для различных приложений; некоторые из них имеют узкую специализацию для определённых задач. Например, B-деревья обычно подходят для создания баз данных, в то время как хеш-таблицы используются повсеместно для создания различного рода словарей, например, для отображения доменных имён в интернет-адреса компьютеров.
Абстра́ктный тип да́нных (АТД)
Это множество объектов, определяемое списком компонентов (операций , применимых к этим объектам, и их свойств). Вся внутренняя структура такого типа спрятана от разработчика программного обеспечения — в этом и заключается суть абстракции. Абстрактный тип данных определяет набор функций, независимых от конкретной реализации типа, для оперирования его значениями. Конкретные реализации АТД называются структурами данных.
В программировании абстрактные типы данных обычно представляются в виде интерфейсов, которые скрывают соответствующие реализации типов. Программисты работают с абстрактными типами данных исключительно через их интерфейсы, поскольку реализация может в будущем измениться. Такой подход соответствует принципу инкапсуляции в объектно-ориентированном программировании. Сильной стороной этой методики является именно сокрытие реализации. Раз вовне опубликован только интерфейс, то пока структура данных поддерживает этот интерфейс, все программы, работающие с заданной структурой абстрактным типом данных, будут продолжать работать. Разработчики структур данных стараются, не меняя внешнего интерфейса и семантики функций, постепенно дорабатывать реализации, улучшая алгоритмы по скорости, надежности и используемой памяти.
Различие между абстрактными типами данных и структурами данных, которые реализуют абстрактные типы, можно пояснить на следующем примере. Абстрактный тип данных список может быть реализован при помощи массива или линейного списка, с использованием различных методов динамического выделения памяти. Однако каждая реализация определяет один и тот же набор функций, который должен работать одинаково (по результату, а не по скорости) для всех реализаций.
Абстрактные типы данных позволяют достичь модульности программных продуктов и иметь несколько альтернативных взаимозаменяемых реализаций отдельного модуля.
Ассоциативный массив
Абстрактный тип данных (интерфейс к хранилищу данных), позволяющий хранить пары вида «(ключ, значение)» и поддерживающий операции добавления пары, а также поиска и удаления пары по ключу.
Стек (LIFO)
Абстрактный тип данных, представляющий собой список элементов, организованных по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»).
Изменяемый набор элементов, формирующийся по правилу «Последним пришел, первым ушел». Может храниться как в векторном представлении (выделенная, не изменяемая область памяти), так и в виде списка (динамически выделяется память под каждый элемент). При векторном представлении стек может переполняться.
Программный вид стека используется для обхода структур данных, например, дерево или граф. При использовании рекурсивных функций также будет применяться стек, но аппаратный его вид. Кроме этих назначений, стек используется для организации стековой машины, реализующей вычисления в обратной инверсной записи.
Для отслеживания точек возврата из подпрограмм используется стек вызовов. Арифметические сопроцессоры, программируемые микрокалькуляторы и язык Forth используют стековую модель вычислений.
Очередь (FIFO)
Абстрактный тип данных с дисциплиной доступа к элементам «первый пришёл — первый вышел» (FIFO, First In — First Out). Добавление элемента (принято обозначать словом enqueue — поставить в очередь) возможно лишь в конец очереди, выборка — только из начала очереди (что принято называть словом dequeue — убрать из очереди), при этом выбранный элемент из очереди удаляется. Очередь может иметь векторную или списковую структуру хранения, но при векторной структуре хранения может произойти переполнение очереди.
Двусвязная очередь
Двусвязная очередь (жарг. дэк, дек от англ. deque — double ended queue; двухсторонняя очередь, двусвязный список, очередь с двумя концами) — структура данных, в которой элементы можно добавлять и удалять как в начало, так и в конец, то есть дисциплинами обслуживания являются одновременно FIFO и LIFO.
Граф
В математической теории графов и информатике граф — это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Граф называется:\ * связным, если для любых вершин u,v есть путь из u в v.\ * деревом, если он связный и не содержит простых циклов.\ * полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.\ * двудольным, если его вершины можно разбить на два непересекающихся подмножества V1 и V2 так, что всякое ребро соединяет вершину из V1 с вершиной из V2.\ * планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.
Свя́зный спи́сок
Базовая динамическая структура данных, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка. Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.
Линейный однонаправленный список
Cтруктура данных, состоящая из элементов одного типа, связанных между собой последовательно посредством указателей. Каждый элемент списка имеет указатель на следующий элемент. Последний элемент списка указывает на NULL. Элемент, на который нет указателя, является первым (головным) элементом списка. Здесь ссылка в каждом узле указывает на следующий узел в списке. В односвязном списке можно передвигаться только в сторону конца списка. Узнать адрес предыдущего элемента, опираясь на содержимое текущего узла, невозможно.
Двусвязный список (двунаправленный связный список)
Здесь ссылки в каждом узле указывают на предыдущий и на последующий узел в списке. По двусвязному списку можно эффективно передвигаться в любом направлении — как к началу, так и к концу. В этом списке проще производить удаление и перестановку элементов, так как легко доступны адреса тех элементов списка, указатели которых направлены на изменяемый элемент.
Кольцевой связный список
Разновидностью связных списков является кольцевой (циклический, замкнутый) список. Он тоже может быть односвязным или двусвязным. Последний элемент кольцевого списка содержит указатель на первый, а первый (в случае двусвязного списка) — на последний.
Дерево
Иерархическая структура элементов, называемыми узлами (вершинами). На самом верхнем уровне имеется только один узел — корень дерева. Каждый узел, кроме корня, связан только с одним узлом на более высоком уровне. Каждый элемент может быть связан ребром с одним или несколькими элементами на следующем, более низком, уровне. Элементы, не имеющий потомков называются листьями. От корня до любой вершины существует один путь.
Любой узел дерева с потомками на всех уровнях так же образует дерево, называемое поддеревом.
M-арное дерево
Число поддеревьев данного узла образует степень узла, максимальное значение m степени всех узлов дерева является степенью дерева. Дерево степени 2 называется бинарным деревом.
Если в дереве на каждом уровне задан порядок следования вершин, то такое дерево называется упорядоченным
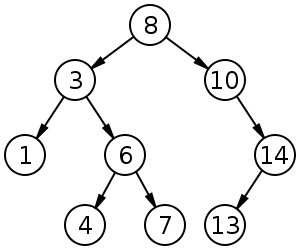
Бинарное дерево поиска
Это двоичное дерево, для которого выполняются следующие условия:
У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
У всех узлов правого поддерева произвольного узла X значения ключей данных больше либо равно, нежели значение ключа данных самого узла X.
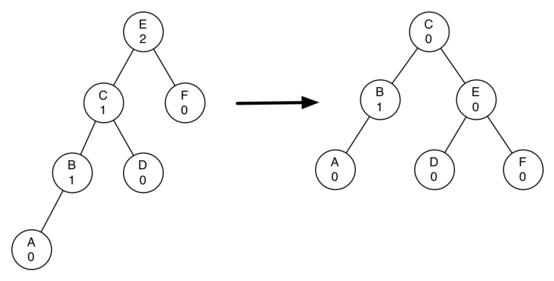
АВЛ-Дерево
Сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
АВЛ — аббревиатура, образованная первыми буквами создателей Адельсон-Вельского Георгия Максимовича и Ландиса Евгения Михайловича.
Красно-чёрное дерево
Это двоичное дерево поиска, в котором каждый узел имеет атрибут цвет, принимающий значения красный или чёрный. В дополнение к обычным требованиям, налагаемым на двоичные деревья поиска, к красно-чёрным деревьям применяются следующие требования:
- Узел либо красный, либо чёрный.
- Корень — чёрный. (В других определениях это правило иногда опускается. Это правило слабо влияет на анализ, так как корень всегда может быть изменен с красного на чёрный, но не обязательно наоборот).
- Все листья(NIL) — чёрные.
- Оба потомка каждого красного узла — чёрные.
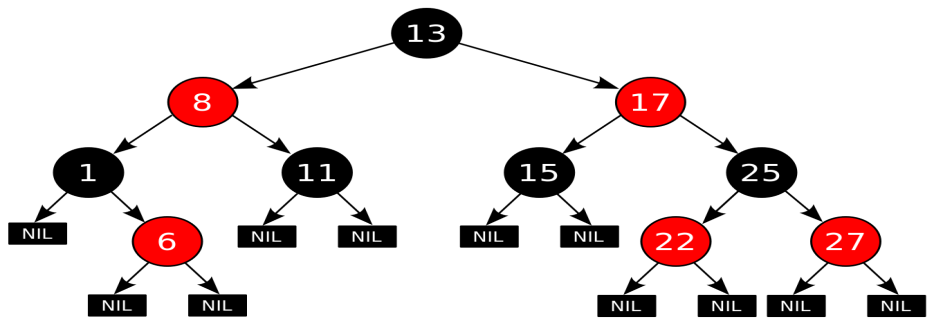Всякий простой путь от данного узла до любого листового узла, являющегося его потомком, содержит одинаковое число чёрных узлов.
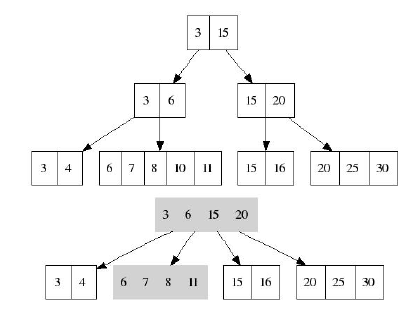
B-дерево
B-дерево – это структура хранения данных, являющаяся разновидностью дерева поиска. Особенностями В-деревьев является: сбалансированность, ветвистость, отсортированность и логарифмическое время работы всех стандартных операций (поиск, вставка, удаление). Сбалансированность означает, что все листы находятся на одинаковом расстоянии от корня. В отличие от бинарных деревьев В-деревья допускают большое число потомков для любого из узлов. Это свойство называется ветвистостью. Благодаря ветвистости, В-деревья очень удобны для хранения крупных последовательных блоков данных, поэтому такая структура часто находит применение в базах данных и файловых системах.
m – порядок В-дерева – это максимальное число потомков для любого узла. Кроме узлов в дереве присутствует ещё одна сущность – ключи. Именно в них и содержится вся полезная информация. Каждый узел дерева можно представить в виде упорядоченной последовательности ”потомок1; ключ1; потомок2; ключ2; … потомок(N-1); ключ(N-1); потомокN”. Важно заметить, что ключи располагаются между ссылками на потомков и, таким образом, ключей всегда на 1 меньше. В организации В-дерева можно выделить несколько ключевых правил:
- Каждый узел содержит строго меньше m (порядок дерева) потомков.
- Каждый узел содержит не менее m/2 потомков.
- Корень может содержать меньше m/2 потомков.
- У корневого узла есть хотя бы 2 потомка, если он не является листом.
- Все листья находятся на одном уровне и содержат только данные (ключи).
